Euler's Equation
Euler's equation is one of most remarkable and mysterious discoveries in Mathematics. Euler's equation (formula) shows a deep relationship between the trigonometric function and complex exponential function.
Discovery of Euler's Equation
First, take a look the Taylor series representation of exponential function,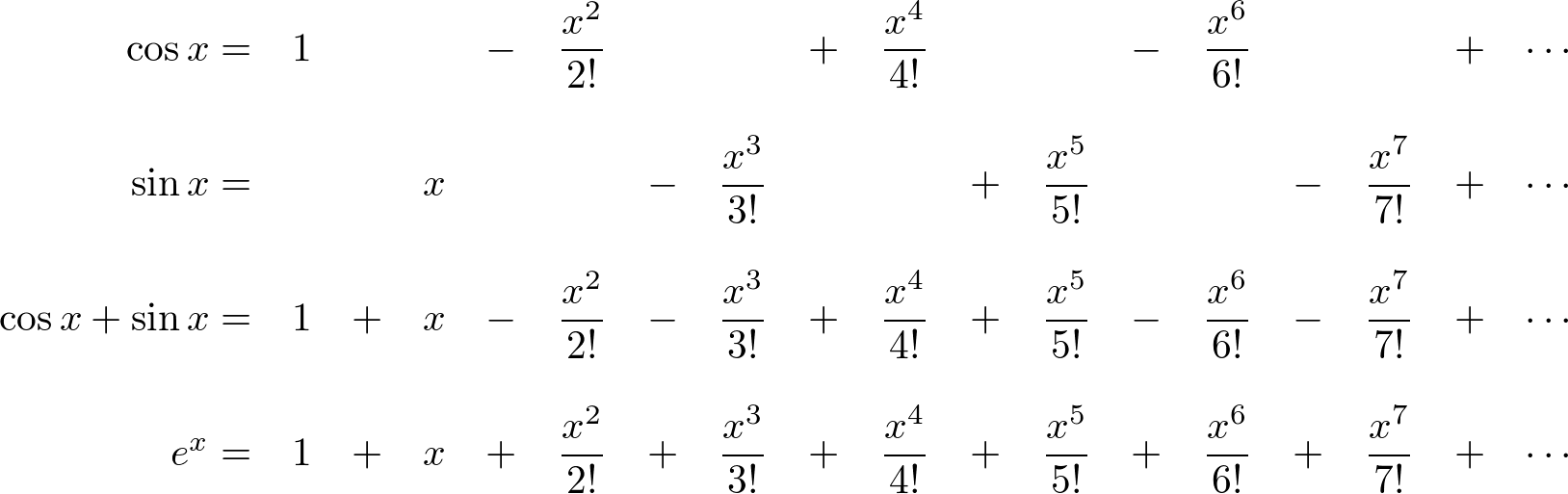 Les't compare
Les't compare Mathematicians had tried to figure out this weird relationship between the exponential function and the sum of 2 oscillating functions. Finally, Leonhard Euler completed this relation by bringing the imaginary number, i into the above Taylor series;
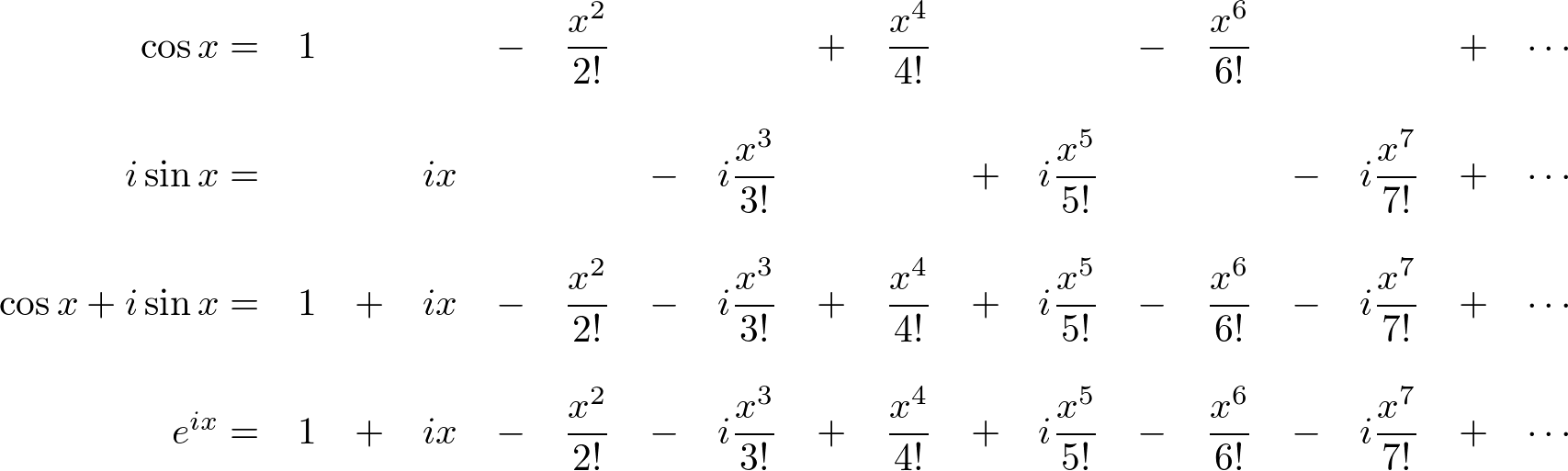 Now, we find out
Now, we find out Graph of Euler's Equation
We know that the exponential function,The following images show the graph of the complex exponential function,
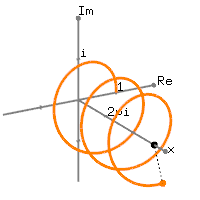
Graph of
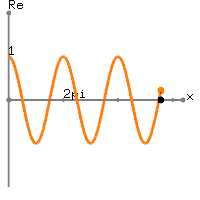
Real number part of
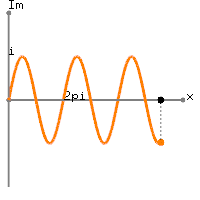
Imaginary number part of
This graphical representation of the complex exponential function, 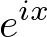 clearly shows the relation to the trigonometric function; the real number part of
clearly shows the relation to the trigonometric function; the real number part of 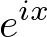 is cosine and the imaginary part of
is cosine and the imaginary part of 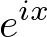 is sine function with the period of
is sine function with the period of 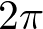 in radians.
in radians.
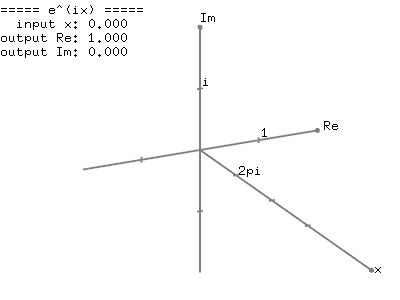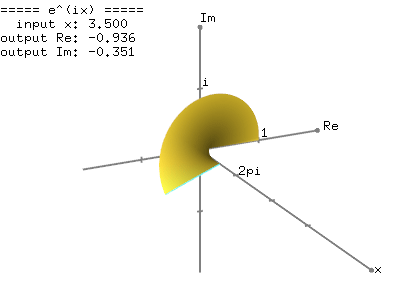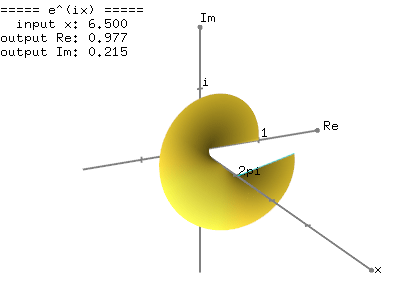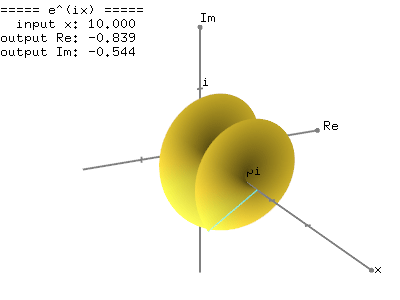
Example of Complex Exponential Function,
Use the mouse cursor to change the view and use 'd' key to change drawing modes.
Meaning of Euler's Equation
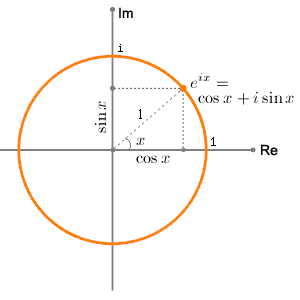
Graph of
It means that raising
The complex exponential forms are frequently used in electrical engineering and physics. For example, A periodic signal can be represented the sum of sine and cosine functions in Fourier analysis, and the movement of a mass attached to a string is also sinusodial. These sinusodial functions can be replaced with the complex exponential forms for simpler computation.
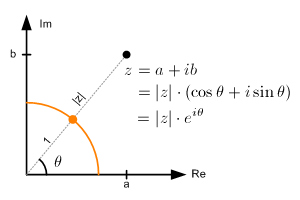
Polar form of a complex number
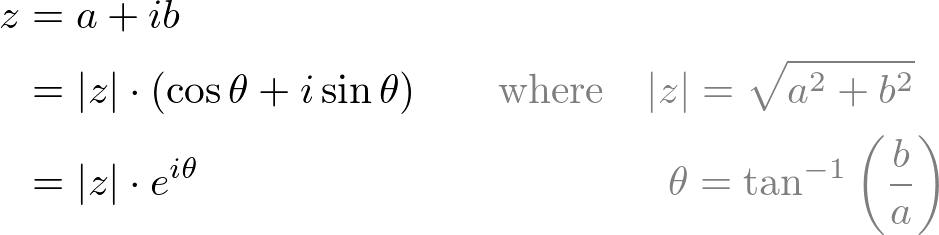 The magnitude (norm), |z| of the complex number is a scalar value and can be rewrtten by using the laws of exponent and logarithm:
The magnitude (norm), |z| of the complex number is a scalar value and can be rewrtten by using the laws of exponent and logarithm: 2D Rotation with Euler's Equation
The multiplication of two complex numbers implies a rotation in 2D space.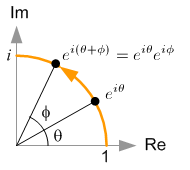
Multiplication implies rotation
When we compare these two complex numbers, we notice that the sum of angles in the imaginary exponential form equals to the product of two complex numbers,
We can extend it to any arbitary complex number. In order to rotate a complex number z = x + iy with a certain angle Φ, we simply multiply
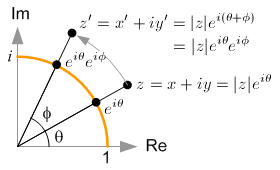
2D rotation of a complex number
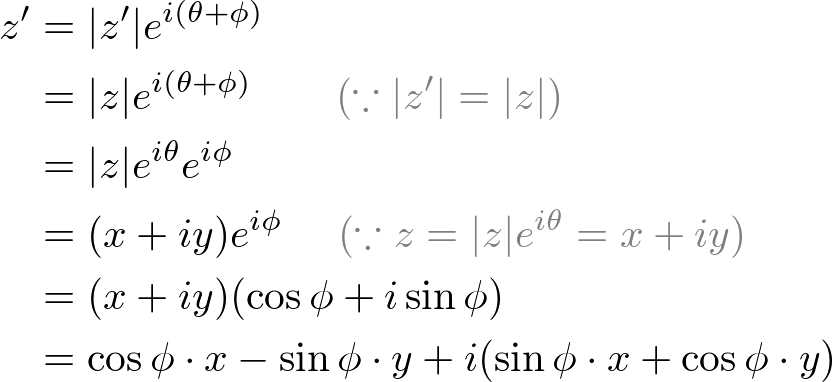
If we re-write it as a matrix form, it becomes a 2x2 rotation matrix that we are familiar with.
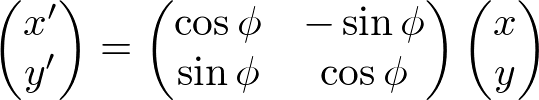
Euler Identity
If we substitute the value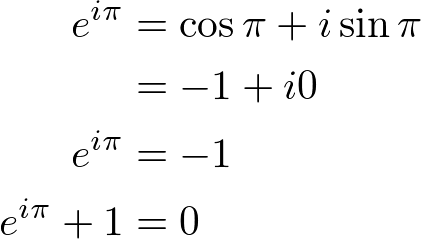 This equation is called Euler Identity showing the link between 5 fundamental mathematical constants; 0, 1,
This equation is called Euler Identity showing the link between 5 fundamental mathematical constants; 0, 1, Logarithmic function is only defined for the domain x > 0. But, Euler Identity allows to define the logarithm of negative x by converting exponent to logarithm form:
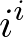 Then raise both sides to the power
Then raise both sides to the power 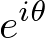 The above equation tells us that
The above equation tells us that Proof of Euler's Equation
This is a proof using calculus. Let's start with the right-hand side only and its differentiate is: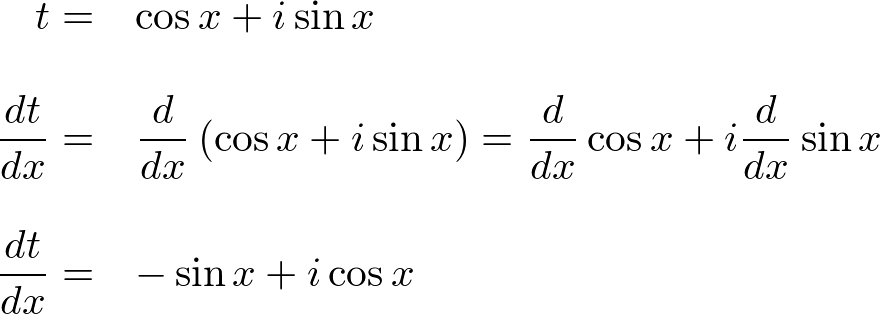
Modify the above equation:
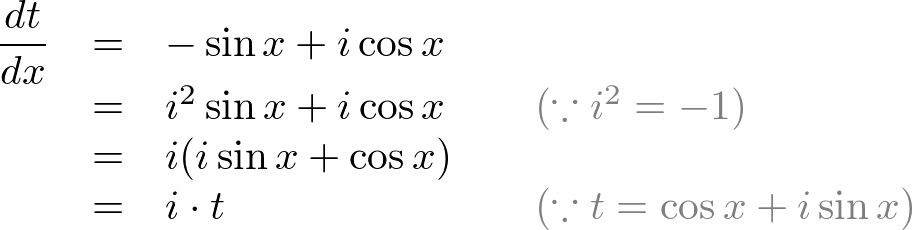
Move t to left-hand side, then apply integral:
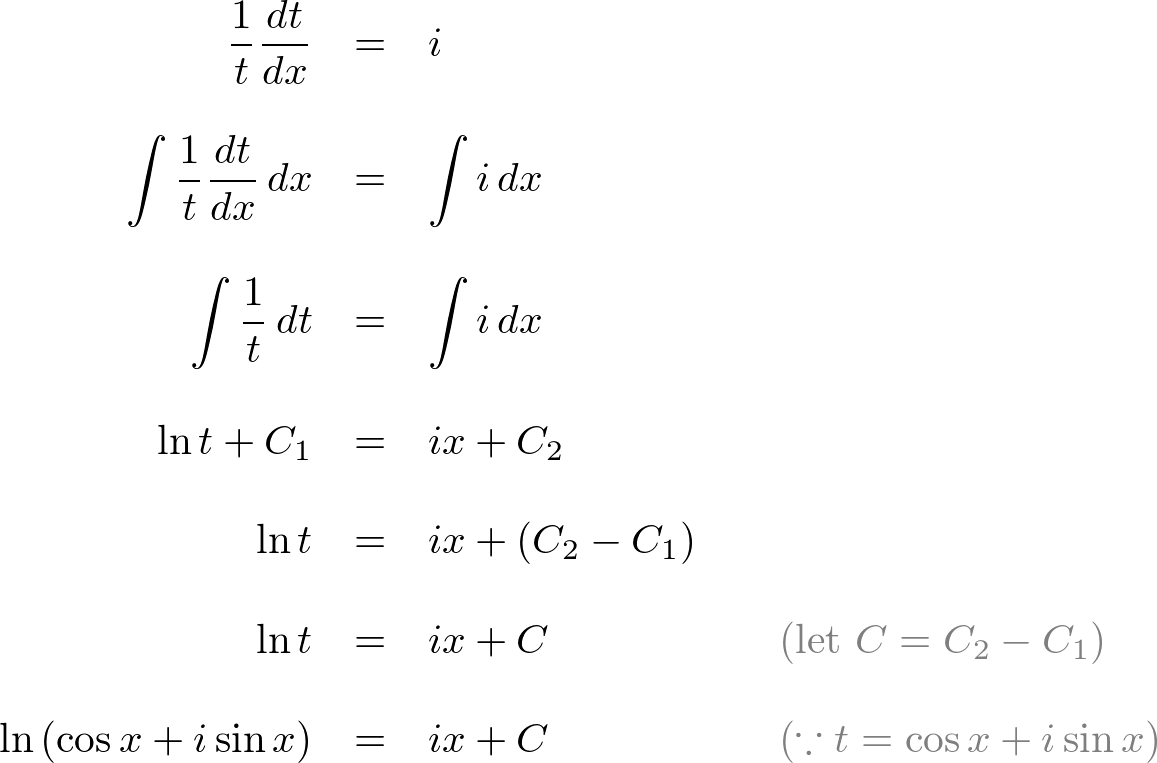
To find constant C, substitute x = 0:
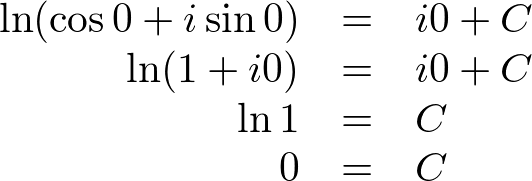
Now, we know C = 0, so the above equation is:
Finally, convert this logarithm form to the exponential form:
No comments:
Post a Comment